A Numerical Approach to Real Algebraic Curves with the Wolfram Language
Bridging the gap between the sophisticated topic of real algebraic curve theory and on-the-spot computation and visualization of real algebraic curves, author Barry H. Dayton uses the Wolfram Language to explore and analyze real curves that often do not have rational points on them. In classical texts, analysis of these types of real curves was only really possible in the theoretical sense, but the Wolfram Language's ability to work with machine numbers, both in calculations and in detailed plots, enables accurate analysis of extremely complicated curves. This book is intended for those with some understanding of calculus and partial derivatives and with basic knowledge of the Wolfram Language.
Available for Kindle Fire, iPad or other tablets. Explore the author's code in his original Wolfram Computational Notebooks, and learn more about Wolfram technology at www.wolfram.com/language.
Contents
- Introduction to Numerical Plane Curves
- Classical vs. Numerical Perspective
- Special Points and Lines
- Gauss Decomposition
- A Classical Interlude
- Fractional Linear Transformations
- Asymptotes, Conics, and Cubics
- Global Plots
- Harnack's Theorem and Newton Hyperbolas
- Final Examples
- Appendix 1: Topics in Numerical Linear Algebra
- Appendix 2: Global Functions
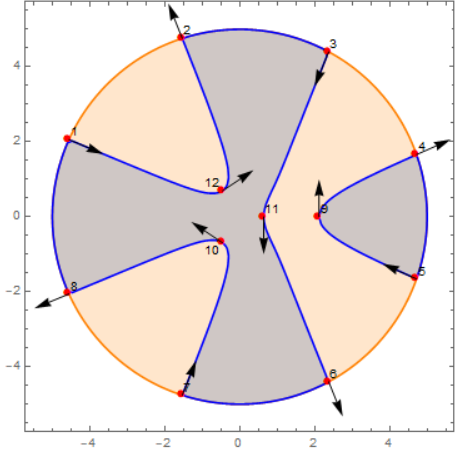
from Chapter 4.3
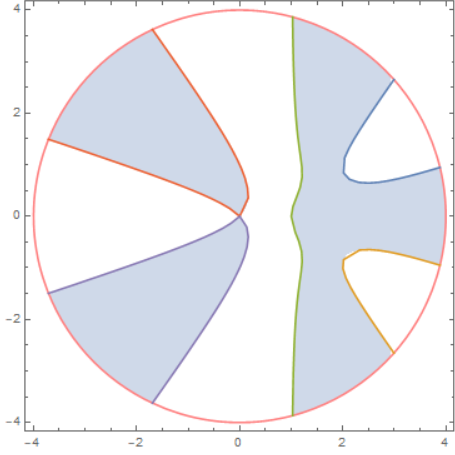
from Chapter 4.7
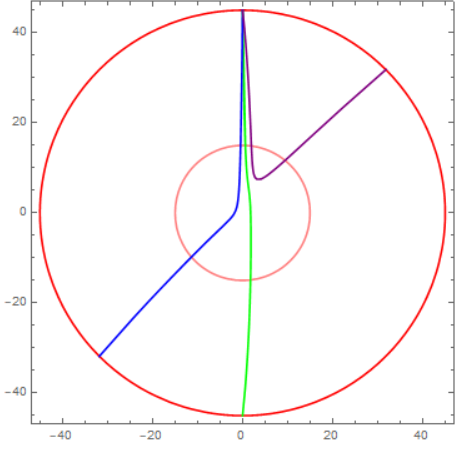
from Chapter 8.4
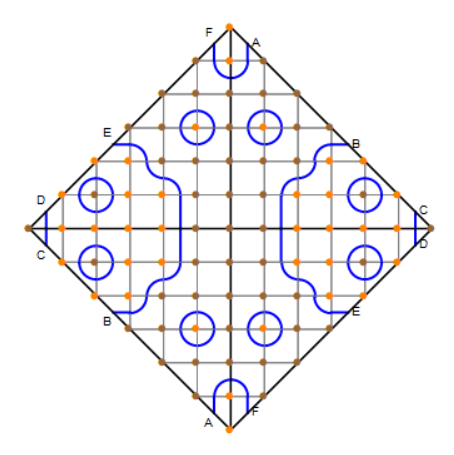
from Chapter 9.4

- Title: A NUMERICAL APPROACH TO REAL ALGEBRAIC CURVES WITH THE WOLFRAM LANGUAGE
- Author: Barry H. Dayton
- Paperback: $55.95 360 pages
- eBook: $34.95 360 pages
- Publisher: Wolfram Media, Inc.
- Publication Date: August 29, 2018
- ISBN-13: 978-1-57955-024-0 (paperback)
- ISBN-13: 978-1-57955-023-3 (eBook)
